Table of contents
Description
GCD (Greatest Common Divisor) or HCF (Highest Common Factor) of two numbers is the largest number that divides both of them.
Example:
We have a = 4 and b = 6. GSD of 4 and 6 is 2. But how do we find it? We can use the super classic way.
The idea is if you create rectangle sizes of a and b. Then we find a larger square that can fill the hole rectangle. However, if we'd have 100 and 200. Do we draw it?
Naive Approach

The main idea is to substruct smaller numbers and find a common divisor.
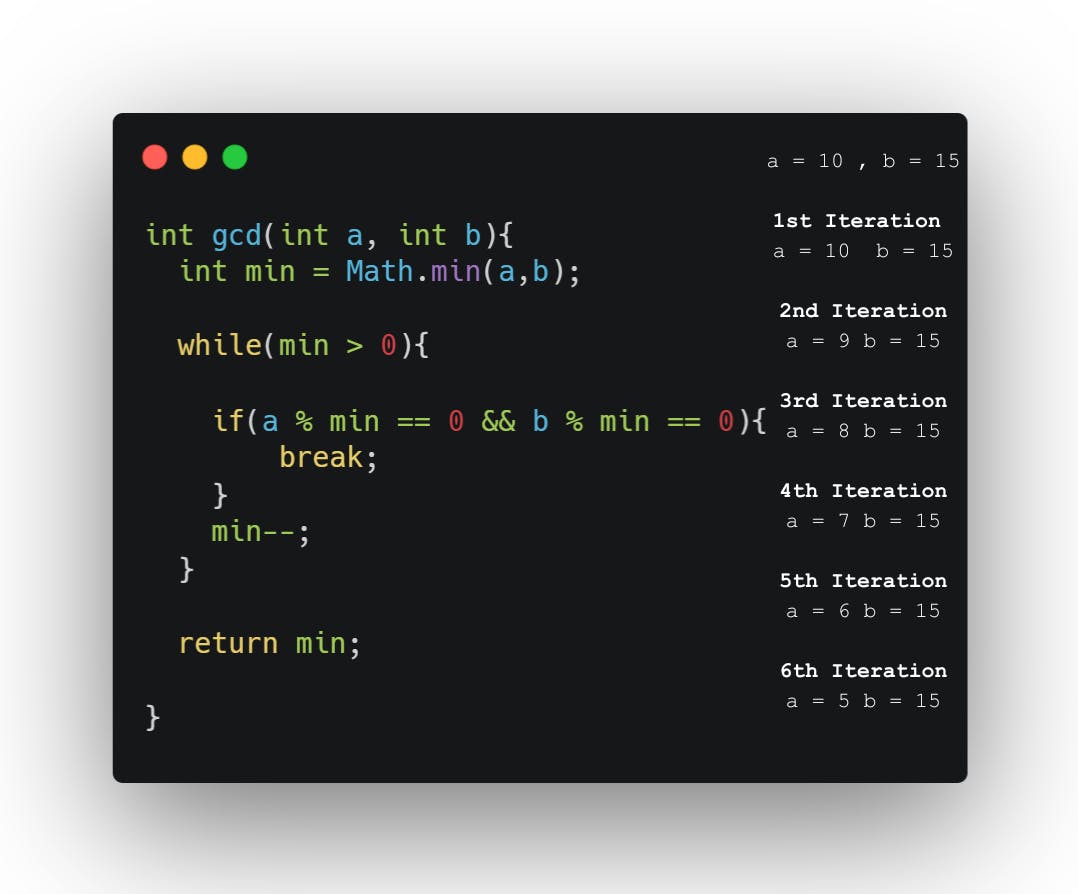
If we look at time complexity that is O(min(a,b). Maybe, in some cases, it's an okay way to solve it problem. However, It's so long.
Euclidean Algorithm
One of the old approach is the Euclidean algorithm by subtraction.
The main idea is to subtract repetitively each time until the result is equal to any one number. If the answer is greater than 1, there is GSD. If the answer is 1, there is no GSD.

Is it faster? Yes, however, we could do it optimized. Let's look at one more variation.
Euclidean Algorithm optimized
Example: a = 12 and b = 15

In this optimized variant we didn't repeat the same operation and we have time complexity: O(log(min(a,b))) that is better than the previous.
Note: If the pass b value is the a value. In the second call, it will swap.
In conclusion
Thank you for your time and don't forget LIKE and COMMENT.
